
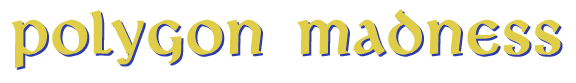
Decagon (10-sided Polygon) Windings
Decagon Winding 1
This winding has a total of five decagons, whose overlapping creates 10 small polygons. The inner layer of small polygons form an attractive snowflake-like shape.
Decagon Winding 2
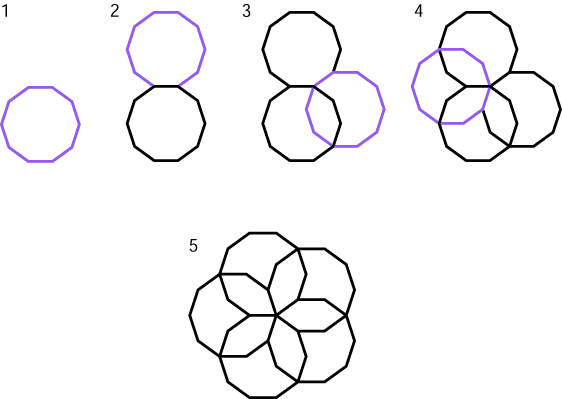
This winding has a total of 10 decagons, whose overlapping creates 50 small polygons. (The innermost circle of polygons is too small to see in the picture above.) The hollow space in the center is actually a small decagon.
Decagon Winding 3
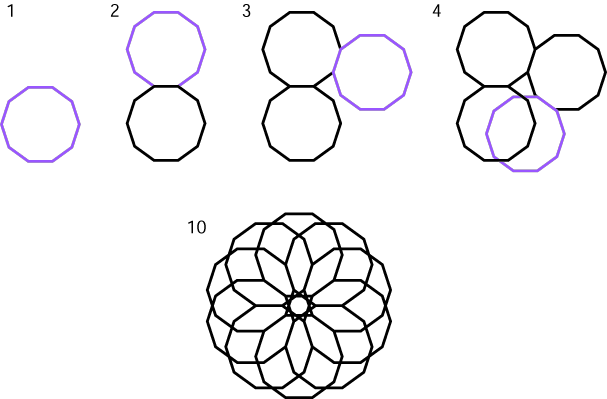
The first non-overlapping winding has half as many polygons as there are sides to each polygon. Octagon Winding 2 also had this property, but Enneagon Winding 3 actually had two-thirds as many polygons as sides to each polygon (6 polygons of 9 sides each).
Decagon Winding 4
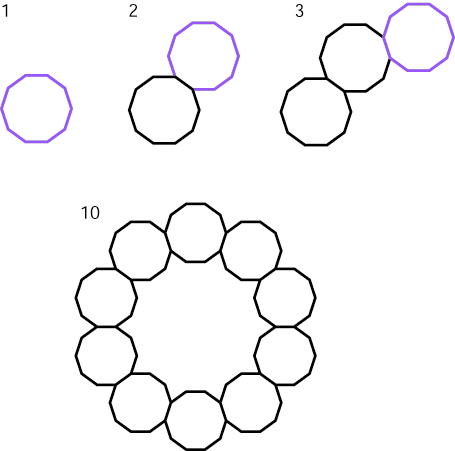
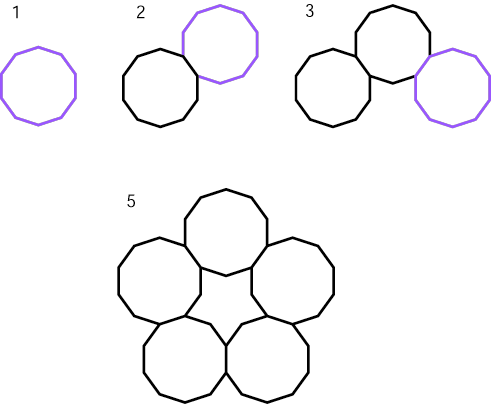
The loosest winding has the same number of polygons as there are sides to each polygon: 10 polygons of 10 sides each.
Conjecture: For polygons with an even number of sides, the loosest winding will always have the same number of polygons as there are sides to each polygon. For polygons with an odd number of sides, the loosest winding will always have twice as many polygons as there are sides to each polygon.
Decagon Nested Windings
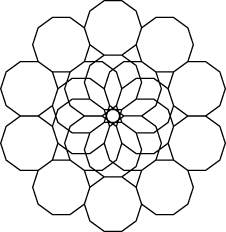
Decagon Winding 2 can be nested within Decagon Winding 4, as shown below:
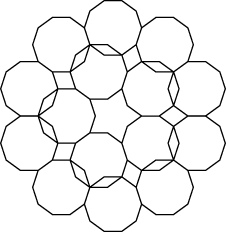
Decagon Winding 3 is a little too large to fit within Decagon Winding 4, but the two windings do overlap regularly at the corners:
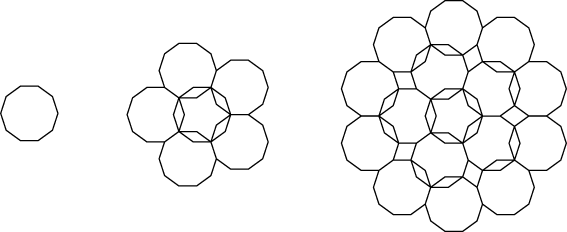
Similarly, a single decagon can nest overlappingly within Decagon Winding 3, which leads to the following progression:
Send comments to jfm.baharna@gmail.com
Return to Baharna.com Home Page
© Copyright 2007 by Joseph F. Morales