Proem

A shocking tale of tilings, semi-regular tilings, demi-regular tilings and rogue polygons yearning to be free.

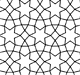
Methods of Construction

The hidden order that lies concealed behind the patterns. A perfect page for conspiracy theorists.

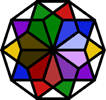
Stained Glass Renderings

Here a selection of designs have been dressed up for a party, enhanced with elaborate lighting, color, or texture, to give an idea of the possible usefulness of these patterns in design.

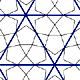
Polygon Windings

Round and round she goes, where she stops—nobody knows! (Until now, that is.)

• What is a Winding?
• Triangle Windings
• Square Windings
• Pentagon Windings
• Hexagon Windings
• Heptagon Windings
• Octagon Windings
• Enneagon Windings
• Decagon Windings
• Hendecagon Windings
• Dodecagon Windings

Single-Unit, Periodic Patterns

A single-unit pattern is one that can be drawn using only a single kind of polygon. Although there may appear to be several kinds of polygons in the pattern, only one of them has to be drawn in. The other shapes consist of the negative space between instances of the primary polygon. For example, in the patern at right, the basic units are all pentagons, which are colored in blue. Between the pentagons, the negative space forms triangles, rhombuses, and six-pointed stars. But no extra lines are needed to form these extra shapes; every line in the picture is part of a pentagon. (If anyone knows a more correct name for this class of pattern, please let me know.) I have generally also adhered to the following rules: the basic unit polygons are always regular polygons, they are all of the same size, and they meet at a single point or along an entire side; that is, a point of one polygon unit does not touch the middle of the side of another.

A periodic pattern is one where the entire pattern can be copied and slid to a different position, set down somewhere else on top of itself, and still have all the points and edges coincide. By "slid" we mean "moved in a single direction without performing any rotations or reflections." Math people call this a "translation." Patterns used in wallpaper and fabrics are generally periodic; otherwise, they would be too complicated to manufacture on a large scale.

Triangle Patterns

The simplest of the polygons, the triangle is easy to combine into larger units that form some unexpectedly complex patterns.

Square Patterns

Squares play particularly well with hexagons, which enable them to be arranged in snakelike, undulating patterns.

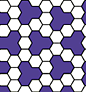
Pentagon Patterns

Pentagons are one of the most difficult shapes to fit into a repeating pattern. Perhaps as a result, the the patterns that are possible turn out to be very dynamic and striking.

Hexagon Patterns

Hexagons are relatively easy to arrange into a variety of patterns with simple and attractive shapes between them.

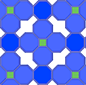
Heptagon Patterns

The negative space in heptagon patterns tends to form bizarre shapes, perhaps because seven is a prime number that doesn't combine naturally with any of the other regular polygons.

Octagon Patterns

Octagons can be viewed as squares with truncated corners, or as the intersection of two squares that were overlaid at a 45 degree angle. Perhaps because of that, the octagons tend to fall into patterns that alternate with squares or that fall into a rectangular grid.

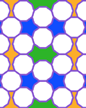
Enneagon Patterns

The nine-sided enneagons don't fit together as readily as you might expect, but they do produce one very interesting unit: a set of six enneagons circled around a six-pointed star.

Decagon Patterns

The ten-sided decagons tend to fall naturally into patterns involving pairs or sets of five.

Hendecagon Patterns

As a prime number, and a relatively large one, the eleven presents unusual difficulties, with only a few arrangements that appear relatively harmonious and natural.

Dodecagon Patterns

The twelve-sided dodecagons play together more gracefully, in more different ways, than any other polygon. Perhaps because twelve is divisible by three, four, and six, it easily develops multiple types of symmetry.

Single-Unit, Aperiodic Patterns

Some shapes lend themselves most easily to patterns that expand outward from a central point. Such patterns are all aperiodic because you can't overlay two copies of the pattern and have them match up unless the center is at the same position in both.

Pentagon Aperiodic Patterns

Pentagons like nothing better to fan outward from a central unit that has five-fold symmetry, such as a pentagon, pentagram, or decagon.