Psychozoan: The Method of Physics

THE METHOD OF PHYSICS

by Henry Nicholls

This space is intended for occasional essays dealing with the way in which science in general, and physics in particular, is structured as an academic discipline. In labeling this method in this way, I intend to distinguish physics as it is taught from how it is practiced, as well as from how it is discussed in lay literature.

Studying physics at the university level, after having had some exposure to several popular renderings of the subject, I was struck by the conceptual leap that the former required, without the least discussion of its intrinsic foreignness (one might even say otherworldliness). Like any person completely immersed in an alien culture, the process of acclimation is inevitably a process of forgetting what it was like to be outside of the paradigm. So, straddling this divide, I have attempted to discuss, to the best of my ability, the underlying reasons (to extent they are clear to me) for the method employed in physics, in a way which I hope the non-physicist can both understand and appreciate.

The problem I have chosen involves a head-on collision of two hard spherical objects of identical mass in a plane (i.e. in two-dimensions). The question is the angle between the paths of the objects after this collision. For ease of visualization, one might consider the collision occurring between two billiard balls on a pool table.

It has been determined through experiment, and also derived from the laws of conservation of momentum and energy, that the trajectories of the billiard balls after the collision always differ by an angle of exactly 90^{^o} (assuming, that is, that their masses are the same and no energy is lost to friction).

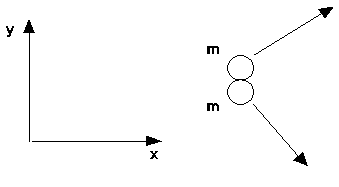
The question is, how do you explain why it is that the angle will always be 90^{^o}. Before I studied physics, I read books on physics directed at the layperson. Such books endeavour to explain problems like this without recourse to mathematics, or through the use of only the most minimal mathematics (basic algebra at most, and as little of that as possible). The problem with such approaches is that they can't even begin to explain why the angle comes out to 90^{^o}. For example, we find a discussion of a similar scenario in Isaac Asimov's well-known work "Understanding Physics: Motion, Sound, and Heat." In his discussion of conservation of momentum, Dr. Asimov uses the example of two pucks colliding. Then we find statements such as

. . . the total momentum of the system would be arrived at by vector addition of the two individual momenta. The two pucks would then bounce in such a way that the vector addition of the two momenta after the collision would yield the same momentum as before.

Although a diagram on the same page clearly shows that the trajectories after the collision differ by 90^{^o}, Dr. Asimov does not refer to this fact in the text. The reason, one may suspect, is that there is no relatively nonmathematical way to describe why this should be so. The result is that the lay reader is never informed of important results, or else treated to explanations of the "and then a miracle occurs" variety.

By contrast, among physicists, this problem is explained in the following succinct fashion:

Momentum is conserved for each component. Working in vector notation, energy conservation and momentum conservation imply that |v_{_{1_i}}||v_{_{2_i}}| cos = |v_{_{1_f}}||v_{_{2_f}}| cos . Since v_{_{2_i}} = 0, the final angle is 90^{^o}.
-- From StudyWare for Physics (Cliff Notes, Inc. 1992)

When, as a beginning physics student on the college level, I achieved a sufficient expertise to be able to understand the problem, such extreme concision appeared to have no purpose other than a perverse desire to explicate the problem in the fewest possible words. However, over time I came to realize the necessity of having sufficient familiarity with the principles which underlay this type of problem so that far more complex problems could be rendered in a format which would not necessitate a forklift.

Thus it seems to me that there should be some useful middle ground between the "user friendly," but ultimately fatally imprecise, lay description and the rigorous, but opaque (at least, to the unitiated), description of the physicists. I will therefore attempt to provide some kind of lay description of the entirety of the answer to this problem as it is understood by physicists. By "lay description" I mean to say that I will explain in detail each step in the solution; however I will avoid (which is to say, wave my hands over) the use of either integral or vector calculus.

Intuitively, we can say how this type of event might play itself out. Physics can tell us how it must occur, at least in the very simplified way in which we have posed the problem.

We begin with one of the foundations of classical mechanics, Newton’s Second Law: F = ma or force is equal to the product of an object’s mass and its acceleration. (As a side note, the centrality of Newton’s Second Law is sometimes expressed in physics circles with the humorous saw that it is the only relation which really needs to be learned, all else in classical mechanics being mere commentary.) But how do we know that F = ma? Well in one sense we don’t. Simply stated physics as formulated by Newton used this mathematic shorthand to describe the natural world of moving and colliding objects. And so by definition, the thing force is the end product of accelerating masses. And more to the point, defining a property force in this way, in concert with a system of other relations, allows you to solve problems you care about. (Assuming you’re a physicist, engineer or someone with a lot of time on your hands). So F = ma is what we start with.

But a relation between force, mass and acceleration isn’t going to get us very far. And the reason for this is the nature of the problem presented. This problem provides us little information other than the fact that it is a closed event. (We are not provided values for the object’s movement or force, which would allow us to manipulate F = ma for our solution.) Objects are moving, they collide and they move apart. However such a closed system of moving objects is the hallmark of the application of conservation principles.

Unfortunately for purposes of our problem there is no conservation law for force. By conservation we mean a law which provides under certain circumstances that a given quality must remain unchanged through the process that is the problem at hand. In linear mechanics there are two such laws: the conservation of momentum and the conservation of energy.

So to begin with, we need to convert what we know (F = ma) into what we need; equations in terms of momentum and energy.

First momentum.

If we think of momentum as something like the value of an object’s movement as a function of its mass (i.e. more massive objects have a greater ability to effect other objects with their movement than less massive objects do, even if they are traveling at the same speed), than it might seem reasonable to say the change in momentum over a give period of time, would describe the force an object imparted. However, this is not how the concepts actually arise in physics. Force is simply defined as this relationship to momentum or p / t = F ( short aside: p is the common abbreviation for momentum). But if we accept this informal way of talking about the relationship, we might also talk about a change in velocity (speed, loosely) over a given period of time, as describing the acceleration of the object or v / t = a.

Now substituting into F = ma we have p / t = mv / t and without regard to the changes over time, p = mv. This is our relation for momentum.

Similarly, for energy (and here our interest is movement or kinetic energy) we start with F = ma. Now force can be reformulated so that it appears as functional output in a given task: work in our lay sense. In physics the equation is as follows W=Fdcos. This tells us that work is the product of a given force through a distance d. is the angle through which the force is imparted. Cosine is a function which continuously changes its value from 0 at 90° to 1 at 0°. And this corresponds to our everyday experience, when we push in a direction perpendicular to the direction of intended action we don’t accomplish anything (no work). Our pushing situation improves until we reach a maximum amount of work at an angle parallel to the direction of intended action. (Incidentally, this type of problem should shed some light on why you studied trigonometry in high school).

Now that we see the connection between force and work, we need to take another conceptual leap between work and energy. In physics work is simply defined as the change in an objects kinetic energy. But the analysis can be viewed in reverse; the total kinetic energy of an object over a give time is the amount of work done on that object over that time. Again as an equation: total KE = W. Now we replace work in our equation with its equivalent value as force and distance discussed above, KE = Fd (for simplicity the cos factor related to the angle of action has been dropped). Replacing force with the its definition we have, KE = mad. Again, using our previous definition of acceleration v / t = a, and adding an analogous one for distance vt = d, with an average value resulting from our change from rest of v / 2. We derive the following: KE = m(v / t)(v / 2)t. Again, ignoring the change over time we are left with KE = mv^² / 2.

Returning finally to the issue of conservation laws, we can apply our postulate that momentum is always conserved. Assuming it is a measurable quantity in the relevant problem, it is the natural means for solving the class of problems in which collisions are prominent. In the way in which physics is conceptualized, all collisions are by their nature problems involving the transfer of momentum.

Unlike momentum, the issue of energy has a further twist. Although energy is also always conserved, it has the unfortunate tendency to readily change its form such that in its final incarnation it may not be a useful tool in problem solving. In a frequent example involving collisions, the objects which collide transfer some part of their kinetic into heat energy (through fiction) when their surfaces interact, and heat energy is not as easily measured as kinetic energy. The class of collisions where such transfers occur are called inelastic. (Think of globs of clay which form a larger, and warmer, mass after being thrown together.) On the other hand collisions where there is no significant interactions (outside forces) at the surfaces, other than the collision itself, are called elastic.

At this point we may reexamine the problem at hand. We note that it involves a collision. We say to ourselves, this probably involves the use of conservation of momentum. We note that the collision is elastic. (Hard surface). We say to ourselves, good I can probably use conservation of energy as well.

Now, conservation of momentum in its pure form.

p_{_{1_o}} + p_{_{2_o}} = p_{_{1_f}} + p_{_{2_f}} (equation 1)

In words this tells us that the sum of the momentums of the two colliding spheres prior to the collision is equal to the sum of their momentums after the collisions.

Note that we have been given a problem where the second sphere is stationary prior to the collision (this sphere has no momentum initially) so that the equation 1 can be immediately simplified as follows:

p_{_{1_o}} = p_{_{1_f}} + p_{_{2_f}} (equation 2)

Stepping back, we recall that p may be written as mv because p = mv. So we rewrite equation 2.

m_₁v_{_{1_o}} = m_₁v_{_{1_f}} + m_₂v_{_{2_f}} (equation 3)

Now the question might very well be asked why would we choose to express momentum in this form. The short answer is that we know what’s coming. Specifically, we know that the equation we will need to use to reduce the variables in equation 3 to a sufficiently small number so that a solution is possible, is the equation for the conservation of energy, and this equation, in the form we will use, is in terms of masses and velocities. (So is equation 3.)

Here is the equation for conservation of kinetic energy:

KE_{_{1_o}} + KE_{_{2_o}} = KE_{_{1_f}} + KE_{_{2_f}} (equation 4)

Again, this tells us that the sum of the kinetic energies of the two colliding spheres prior to the collision is equal to the sum of their energies after the collisions. And again there is no kinetic energy initially for the second sphere, so equation 4 can be simplified, as occurred with equation 1.

KE_{_{1_o}} = KE_{_{1_f}} + KE_{_{2_f}} (equation 5)

Again, substituting the derived value KE = mv^² / 2 we can thereby rewrite equation 4 as follows:

m_₁v^²_{_{1_o}}/ 2 = m_₁v^²_{_{1_f}}/ 2 + m_₂v_{_{2_f}}/ 2 (equation 6)

Now further simplification of equations 3 and 6 is possible. Initially, we were provided with the information that both spheres were of equal mass. That being the case the problem is not mass sensitive, and we may factor out mass from both equation 3 and 6, leaving these equations (we can also factor out 1/2 out of each term in equation 6):

v_{_{1_o}} = v_{_{1_f}} + v_{_{2_f}} (equation 7)

v^²_{_{1_o}} = v^²_{_{1_f}}+ v^²_{_{2_f}}(equation 8)

Now, earlier mention was made of idea that we were engaged in these algebraic manipulations for the purpose of deriving an equation or equations from the facts given that was solvable. Algebra dictates that we can solve equations where the number of variable to be solved is equal to the number of independent equations where these variables are related. Thus, y = 2 + x and x = y -7 can be solved for x and y (two variables and two equations).

But what is it we want to know? The angle between the trajectories of our spheres after their collision. Well, neither equation 7 nor 8 appear to contain variables in terms of relative angles. But in fact they do.

Each variable above labeled v for velocity is not only reflective of the absolute speed of the object, but also stands for the relative direction of each object. In the terminology of mathematics quantities that have two component parts are called vectors, and velocity is a vector.

But there is considerably more to velocity’s vector nature than its two components. By all appearances equation 8 might merely be the result of squaring equation 7. Not so.

Consider the quantity (3 + x). When we square this quantity we do not get 3^² + x^², instead we must multiply each term by each term and the solution is 3^² + 6x + x^². Similarly, if we square each term in equation 7 we don’t get equation 8, but the following result, because in reality we are dealing with two components in the process of squaring each term:

v^²_{_{1_o}} = v^²_{_{1_f}}+ 2v_{_{1_f}}v_{_{2_f}} + v^²_{_{2_f}}(equation 9)

Now, we can readily see that simply subtracting equation 8 from equation 9 will reduce significantly the complexity of our equation. ( And note, if squaring 7 produced an identical equation to 8 we would be left with no terms.) Fortunately, applying the correct method of multiplication, we are left with the following result:

0 = 2v_{_{1_f}}v_{_{2_f}} (equation 10)

Now the directional component of our velocity vector needs to be examined. By definition there are two ways of multiplying vectors in the directional sense. One way (what is called the scalar product) simply involves multiplying the magnitudes of the relevant vectors and taking the cosine of the angle between them. In short vector a × vector b = abcos. What this produces is a simple number without a directional component ( a scalar). (This works out if one realizes that a and b are just numbers, and the cosine of an angle is also a number.) But, as a computational tool, what this method also does is allow us to calculate a vector’s length if we know another vector’s length and the angle between them, or the angle between two vectors if we know their lengths, through straight forward algebra.

Best of all, at least for purposes of this problem, is the ability of this method to calculate the value of certain angles even where nothing is known about the lengths of the vectors.

Returning to equation 10, we see that the multiplication of 2v_{_{1_f}} ^. v_{_{2_f}}=2v_{_{1_f}}v_{_{2_f}}cos according to our definition of the scalar product. But we also know (from equation 10) that 2v_{_{1_f}}^. v_{_{2_f}}= 0. So,

0 = 2v_{_{1_f}}v_{_{2_f}} cos (equation 11)

Well we know v_{_{1_f}} and v_{_{2_f}} 0 (our spheres are moving after all after the collision), and 2 0, so cos must equal 0, because some multiple of the left side of equation 11 must equal 0. And cos = 0 only exists when equals 90°.

Now we know. In every inelastic collision between spheres of equal mass the angle between their resultant trajectories must be 90°. If you have a pool table, give it a try.

Seriously, what seems significant in this exercise to me is the clear hierarchy of problem solving that even this relatively simple problem demands. The answer lies in following a firm plan of classifying each piece of information. So, we first see a collision which tells us that certain conservation laws and the equations derived from them will be used. Next, we see that the equations must be modified in a way which will leave us with the variables which relate to the problem to be solved. Lastly, we use the physical parameters of the problem to identify the specific modification which is most useful in the context of solving this type of problem.

I hope that the reader will understand that this article is meant to provide some idea of the process that a physicist would go through in solving this type of problem. Although that process has been rendered in much more basic math than would actually be used, and has been described in much greater detail.

In closing, I would like very much to hear from non-scientists regarding their impressions of this description of the way in which physics is structured. And for any physicist who might come across this piece, please feel free to forward to me discussion points, as well as any and all errors you find. (I feel confident that I have provided them in abundance.)

About the author: Henry Nicholls has studied law and physics and works in insurance defense. He recently shaved his head in an attempt to look "cool." Please write to tell him what a bad idea this really was.

Return to Psychozoan Home Page

Send comments to jfm.baharna@gmail.com