
Dodecagon (12-sided Polygon) Windings
What a difference a side can make. While the 11-sided hendecagon is crusty and recalcitrant, unwilling to play with others, the 12-sided dodecagon is the model of amiability. There are four different ways of winding the dodecagon without overlaps, a numerous ways to repeat it across a plane.
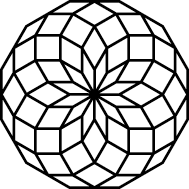
Windings A, B, and C
Winding A is made of 12 dodecagons, forming five layers of petals for a total of 60. From Windings B and C, you can see that dodecagons also naturally group in clusters of 3 or 4. Is this because 12 is divisible by 3 and 4?
 |
 |
 |
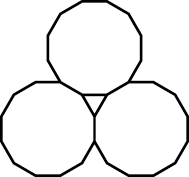
Winding D
Winding D gives us a grouping of 6 nonoverlapping dodecagons. Again, is this because 12 is divisible by 6?
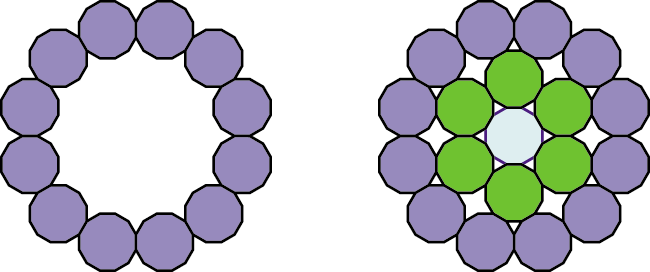
As an added bonus, the space in the middle is just large enough to hold another dodecagon of the same size, that is not part of the winding itself.
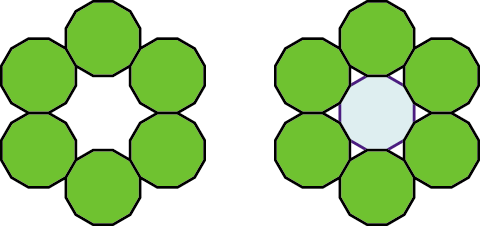
Winding E
With Winding E, we again have a pattern of 12 dodecagons, just as with Winding A. Only in this case, they don't overlap.
Within this big circle, you can fit dodecagons of the same size, arranged in Winding D. With the addition of another dodecagon in the center, you get an arrangement that looks like a target.
Approaching Circularity
Though hendecagons are the most flexible polygons we have examined, there is a downside. With 12 sides, the figure is starting to look almost circular. This makes the arrangements far less dramatic than figures made from pentagons and so forth. It appears that we are approaching a point of diminishing returns, at least from the point of view of visual interest. Because of this, I haven't explored figures with 13 or more sides.
Send comments to jfm.baharna@gmail.com
Return to Baharna.com Home Page
© Copyright 2007 by Joseph F. Morales